In mathematics, rational and irrational numbers are real numbers used to represent integers. The integers that are non-recurring or non-terminating are irrational numbers. While the integers that are recurring and are finite or terminating are referred to as rational numbers.
In this post, we will learn about the definitions and how to calculate rational and irrational numbers with examples.
What are rational numbers?
A number that is written in the form of a ratio or fraction like p/q where both p & q are integers and the denominator never be zero is said to be a rational number. Keep in mind that rational numbers and fractions are two different terms.
The whole numbers are written in fractions while integers are written in the numerator and denominator to make a p/q form in rational numbers.
Following are a few examples of rational numbers.
21/34
14/91
-51/72
0.09 or 9/100
-0.004 or -4/1000
What are irrational numbers?
A number that can’t be written in the form of a ratio or fraction like p/q where both p & q are integers and the denominator never be zero is known as an irrational number. In simple words, the contradiction of rational numbers is known as irrational numbers.
some examples of irrational numbers are pi, √2, √3, Euler number e, and golden ratio φ.
How to identify rational and irrational numbers?
To identify rational and irrational numbers, we have to know about rational and irrational numbers. The numbers that are given for identification that either rational or irrational numbers. Apply the definitions of both terms for accurate results.
You can also use the best electrical engineering calculator or rational or irrational calculator to identify the numbers. To use a rational number calculator, follow the steps below.
Step 1: Select the operator either you want to calculate a fractional number or a square root number.
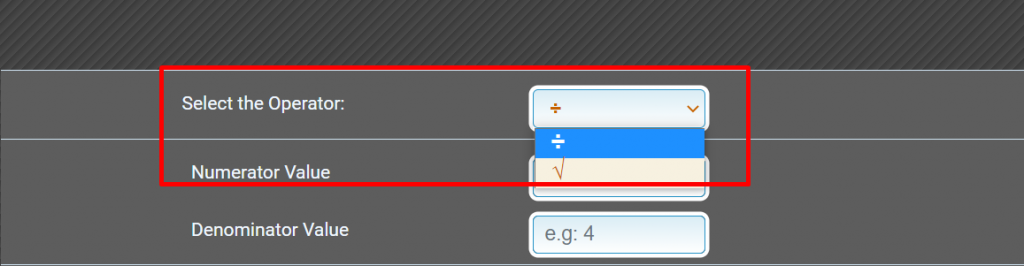
Step 2: Put the numerator and denominator value in the case of the fraction. And put the number and index value in case of square root.

Step 3: Hit the calculate button below the input box to identify the number.
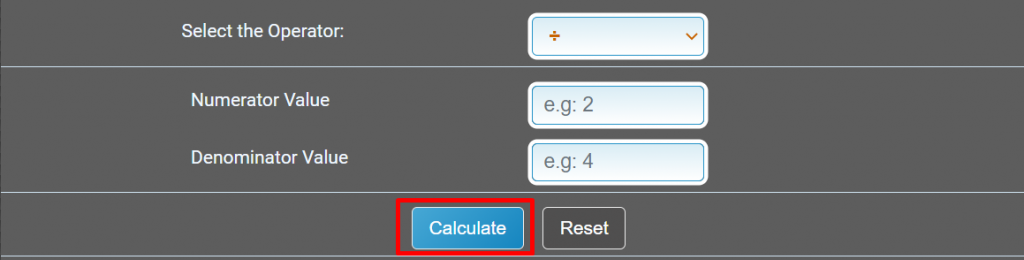
Step 4: The result will show below the calculate button.

Example 1
Is 0.45201452014520145201452014520145201…. a rational or irrational number?
Solution
Step 1: Write the given non-terminating number.
0.45201452014520145201452014520145201….
Step 2: Now check the given number whether it is repeating or non-repeating.
0.45201452014520145201452014520145201….
The set of decimals 45201 is repeating again and again so the given number is repeating.
Step 3: Write the result.
Since the number that is non-terminating and repeating is known as a rational number.
So, 0.45201452014520145201452014520145201…. is a rational number.
Example 2
Is 2.345678912301245897654…. a rational or irrational number?
Solution
Step 1: Write the given non-terminating number.
2.345678912301245897654….
Step 2: Now check the given number whether it is repeating or non-repeating.
2.345678912301245897654….
The set of decimals is not repeating again and again so the given number is non-repeating.
Step 3: Write the result.
Since the number that is non-terminating and non-repeating is known as an irrational number.
So, 2.345678912301245897654…. is an irrational number.
Example 3
Is 1/3 a rational or an irrational number?
Solution
Step 1: Write the given fraction and convert it into decimal form.
1/3 = 0.33333333333….
This is a non-terminating number.
Step 2: Now check the given number whether it is repeating or non-repeating.
0.33333333333….
Since the set of 3 is repeating continuously so we can conclude that the above non-terminating number is repeating.
Step 3: Write the result.
Since the number that is non-terminating and repeating is known as a rational number.
So, 1/3 = 0.33333333333…. is a rational number.
Example 4
Is 11/7 a rational or an irrational number?
Solution
Step 1: Write the given fraction and convert it into decimal form.
11/7 = 1.57142857143….
This is a non-terminating number.
Step 2: Now check the given number whether it is repeating or non-repeating.
1.57142857143….
Since the set of decimals is repeating so, we can conclude that the above non-terminating number is repeating.
Step 3: Write the result.
Since the number that is non-terminating and repeating is known as a rational number.
So, 11/7 = 1.57142857143…. is a rational number.
Some other examples of rational and irrational numbers are given below.
| Questions | Answers |
| Is 13/15 a rational number or an irrational number | Rational |
| Is 0.5689 a rational number | Yes, it is rational |
| Is square root 3 a rational number or an irrational number | Irrational |
| Is 21 a rational number | Yes, it is rational |
| Is 3.14159 an irrational number | Yes, it is irrational |
| Is square root 2 a rational number | No, it is not rational |
| Are golden ratio and Euler number a rational number | No, it is not rational |
| Is 0.76 a rational number | Yes, it is rational |
| Is 0. 45678945382.. a rational number | No, it is not rational |
| Is 0. 45678945382.. an irrational number | Yes, it is irrational |
| Is 22/7 a rational number or an irrational number | Rational |
| Is 1/30 a rational number or an irrational number | Rational |
What is the difference between rational and irrational numbers?
Here are some differences between rational and irrational numbers.
| Rational number | Irrational number |
| A number that is written in the form of a ratio or fraction like p/q where both p & q are integers and the denominator never be zero is said to be a rational number. | It contradicts the results of a rational number. |
| Example are 2/3, 4/9, -5/7, 0.9 or 9/10, and -0.4 or -4/10 | Examples are pi, √2, √3, Euler number e, and golden ratio φ |
| Decimals are terminating. | Decimals are non-terminating. |
| A non-terminating and repeating decimal term is known as a rational number. | A non-terminating and non-repeating decimal term is known as an irrational number. |
| It has a set of whole numbers, natural numbers, and integers. | It has no set of numbers. |
Summary
Rational and irrational numbers are real numbers and are used to represent the numbers in the number system. You can grab all the basics of rational and irrational numbers by learning this post.
Read more about What is Percentage Yield?
